8.8.3. DataObject

The class DataObject (part of the library dataObject) provides a n-dimensional matrix that is used both in the core of itom as well as in any plugin. The n-dimensional matrix can have different element types. These types and their often used enumeration value are defined in the file typeDefs.h and are as follows:

Typedef	Enumeration	Description
ito::int8	ito::tInt8	8bit, signed, fixed point
ito::uint8	ito::tUint8	8bit, unsigned, fixed point
ito::int16	ito::tInt16	16bit, signed, fixed point
ito::uint16	ito::tUint16	16bit, unsigned, fixed point
ito::int32	ito::tInt32	32bit, signed, fixed point
ito::uint32	ito::tUint32	32bit, unsigned, fixed point
ito::float32	ito::tFloat32	32bit, single-precision floating point
ito::float64	ito::tFloat64	64bit, double-precision floating point
ito::complex64	ito::tComplex64	real and imaginary part is float32 each
ito::complex128	ito::tComplex128	real and imaginary part is float64 each
ito::rgba32	ito::tRGBA32	color value (red, green, blue, alpha - 8bit each)

The last two dimensions of each DataObject are denoted plane and physically correspond to images. Since no one-dimensional DataObject is available, each DataObject at least consists of one plane. In order to also handle huge matrices in memory, usually the different planes are stored at different locations in memory. Internally, each plane is an OpenCV matrix of type cv::Mat_<type>, derived from cv::Mat. Therefore every plane can be used with every operator given by the OpenCV-framework (version 2.3.1 or higher). This kind of DataObject and its way of allocating memory is called non-continuous.

In order to make the DataObject compatible to matrices that are allocated in one huge memory block (like Numpy arrays), it is also possible to make any DataObject continuous. Then, a huge data block is allocated, such that all planes lie consecutively in memory. This reallocation is implicitly done, when creating a Numpy-array from a non-continuous DataObject.

DataObject can be declared in different possible ways with different dimensions and different data types.

Let’s take an example of a 3x2x5 data object. It can be imagined as shown in the figure below.

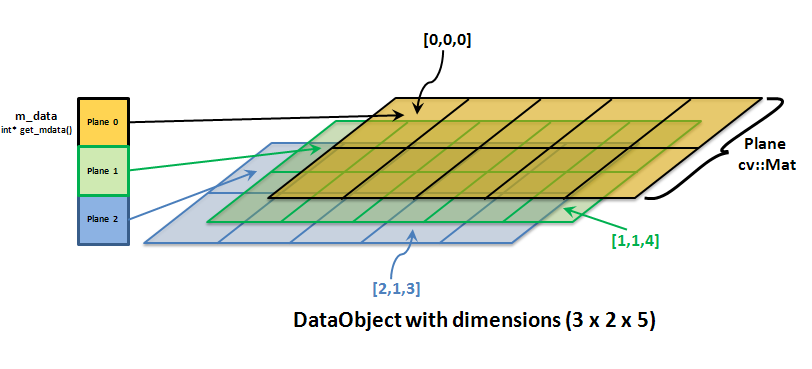
As we can see in this figure, each plane is of a type cv::Mat class from OpenCV library which we know. The internal index of a specific plane can safely be retrieved using the method seekMat(). Usually the i-th plane has got the index i, however in case of data objects representing a subpart or region of interest of another data object, the i-th plane with respect to the current region of interest can in reality have a bigger index than i. The pointers to all planes are stored in one linear vector, represented by the array member m_data. It is accessible via get_mdata() and is of type int*. However, it can directly and safely be type-casted to cv:Mat* or cv::Mat_<Type>. Please read the section Direct Access to the underlying cv::Mat to understand this concept in detail with a working example.

The following code creates an empty data object with no dimensions (0) and no type (0).

ito::DataObject d0;
std::cout << "empty data object: \n";
std::cout << " dimensions: " << d0.getDims() << "\n";
std::cout << " type: " << d0.getType() << "\n" << std::endl;

The number of dimensions of this data object are obtained by getDims(), whereas its type value in terms of the enumeration above is returned via getType().

The following code creates a 2 dimensional data object of dimensions Y=2, X=5 and of type float32.

ito::DataObject d1(2,5, ito::tFloat32);
std::cout << "2x5 data object, float32: \n";
std::cout << " dimensions: " << d1.getDims() << "\n";
std::cout << " type: " << d1.getType() << "\n";
std::cout << " size: " << d1.getSize(0) << " x " << d1.getSize(1) << "\n";
std::cout << " total: " << d1.getTotal() << "\n";
std::cout << d1 << std::endl;

The size of the specific dimensions is obtained by getSize where the argument is the index of the dimensions (x is always the last dimension with the biggest index value). getTotal returns the total number of elements within this data object.

8.8.3.1. Creating a data object

For creating a data object in C++, there are different constructors available. They are discussed in this section.

An empty data object is created using the argument-less, default constructor:

ito::DataObject d1;

It has no dimensions and contains no elements. For creating a two or three dimensional data object of a desired type, filled with arbitrary, but not random values, use one of the following constructors:

ito::DataObject(const int sizeY, const int sizeX, const int type); //type is one of the enumeration values
ito::DataObject(const int sizeZ, const int sizeY, const int sizeX, const int type, const unsigned char continuous = 0);

The optional continuous parameter indicates, whether a continuous object (one block in memory) should be allocated (1), or not (0, default). For higher dimensional objects, there is a constructors that requires an allocated integer array that contains the sizes of all dimensions:

ito::DataObject(const unsigned char dimensions, const int *sizes, const int type, const unsigned char continuous = 0);
//e.g.
int sizes[] = {3,4,5,2};
ito::DataObject d1(4,sizes,ito::tFloat32);

One other important constructor is - of course - the copy constructor. It creates a shallow copy of an existing data object. A shallow copy means, that both data objects share the same data (hence the array itself), but the header information is separated (dimensions, sizes…). All meta information is shared as well (axes descriptions, scales, protocol…). If a value of the one object is changed, the corresponding value in the other object is changed as well. The principle of using shallow copies is a common principle in C programming and highly used in OpenCV. It speeds up the calculation and requires less memory. On the other hand, you need to take care about the values. If you want to have a so called deep copy of an object, use the copy method.

If you know what you do, you can also create a data object from multiple cv:Mat of the same type and size. If so, you need to have an array of all cv::Mat (each corresponding to one plane). The created data object then creates a fast shallow copy of all planes and uses them:

ito::DataObject(const unsigned char dimensions, const int *sizes, const int type, const cv::Mat* planes, const unsigned int nrOfPlanes);

//e.g.
cv::Mat planes[] = { cv::Mat::ones(50,50,CV_8U), cv::Mat::zeros(50,50,CV_8U)};
int sizes[] = {50,50};
ito::DataObject d1(2, sizes, ito::tUInt8, planes, 2);

Furthermore, there are several constructors to create data objects whose values are already set to the values of a given array. The reader is referred to the detailed documentation of class ito::DataObject for this.

8.8.3.2. Addressing the elements of a data object

Now, we know how to create a data object, so lets have a look at how can one address the elements of a data object. Sometimes it is necessary to read or set single values in one matrix, sometimes one want to access all elements in the matrix or a certain subregion. Therefore, the addressing can be done in one of the following ways:

8.8.3.2.1. Direct access of one single element of a Data Object using at<_Tp>() method

ito::DataObject d1(2,5, ito::tFloat32);
d1.at<ito::float32>(0,1) = 5.2;
std::cout << "d1(0,1) = " << d1.at<ito::float32>(0,1) << "\n" << std::endl;

Here, the addressing is done by the member method at(), which is pretty similar to the same method of the OpenCV class cv::Mat. The at() method can either be used to get the value at a certain position or to set value at that position in a data object. There are special implementations of at() for addressing values in a two- or three-dimensional data object, where the first argument always is the z-index (3D), followed by the y-index and the x-index. All indices are zero-based, hence the first element can be referred by addressing 0th position in every dimension.

Note

The at() method is templated where the template parameter must correspond to the type of the corresponding data object.

Let’s try to summarize some pros and cons of this method.

Advantages

• This method gives flexibility to a developer to directly access any element of a data object.

• A developer can also access a part of a data object as well using at() method as described in Direct Access to the underlying cv::Mat.

Drawbacks

• Developer has to implement the code under the nest of if…else conditions if one needs to access the whole data object.

• It is slow for accessing a lot of values of the matrix compared to the other possible methods.

8.8.3.2.2. Addressing elements of a data object using row pointer

When one needs to iterate through certain regions of a data object, then the previous method of accessing a data object using at method seems quite insufficient. In such case, one can define a row pointer for each row in matrix and work with row pointer to address elements of a data object in the following way.

ito::DataObject d1(3,5, ito::tInt16);
int planeID = d1.seekMat(0);   //get internal plane number for the first plane
ito::int16 *rowPtr = NULL;
int height = d1.getSize(0);
int width = d1.getSize(1);
for(int m = 0; m < height; m++)
{
    rowPtr = (ito::int16*)d1.rowPtr(planeID,m);
    std::cout << "Row " << m << ":";
    for(int n=0; n < width; n++)
    {
        rowPtr[n] = m;                 //accessing each element of data object with row pointer
    }
}
std::cout << d1 << std::endl;

Here, seekMat() method gets the internal plane number of the 1st plane in line #2. In line #8, the pointer to the data array of the m-th row in the 2D-plane is obtained and safed in rowPtr. By iterating through the array given by the rowPtr, each element in this row can be read and set to a specific value.

To use this row pointer method for data objects more than 2 dimensions, following code can be used.

ito::int16 *rowPtr1= NULL;
int dim1 = d1.getSize(0);
int dim2 = d1.getSize(1);
int dim3 = d1.getSize(2);
int dim4 = d1.getSize(3);
int dim5 = d1.getSize(4);
int dataIdx = 0;
for(int i=0; i<dim1; i++)
{
    for(int j=0; j<dim2; j++)
    {
        for(int k=0; k<dim3; k++)
        {
            dataIdx = d1.seekMat(i*(dim2*dim3) + j*dim3 + k);
            for(int l=0; l<dim4; l++)
            {
                rowPtr1= (ito::int16*)d1.rowPtr(dataIdx,l);
                for(int m=0; m<dim5; m++)
                {
                    //Assigning unique value to each element of d1.
                    rowPtr1[m] = yourValue;
                }
            }
        }
    }
}

Note

Here dataIdx represents the number of the plane in the matrix. The formula in line #14 assigns a non repeating increasing value to dataIdx such that each plane of the data object can be pointed out without any overlapping.

Note

Usually it is not allowed to use the rowPtr to access the items of one of the following rows, since it is not sure if the elements of the next row directly follow to the last value of this row. For instance, this is not the case, if the current plane represents a region of interest of a bigger plane. You can only iterate through one entire plane using the row-pointer of the first row if the plane is continuous. This can be checked by the continuous property of the cv::Mat that represents this plane.

Some advantages and disadvantages of using this method are given in the section below.

Advantages

• This method is the most efficient way to access the data object.

• This method gives flexibility to access some rows or the full data object at once.

Drawbacks

• Complex implementation. One needs deep understanding of pointers to implement this method to access data object.

• This is not an advisable method if one needs to access a few elements of the data object which are not in sequence.

8.8.3.2.3. Assigning a single value to all elements of a data object

One can assign a single value to all elements of a data object using the assignment operator “=” in the following way. Here we will also have a look on how to declare a 5 dimensional data object and assign a single floating point value to each element of the data object.

int temp_size[] = {10, 12, 16, 18, 10};
ito::DataObject d1(5,temp_size,ito::tFloat32);
d1 = 3.7;
std::cout << d1 << std::endl;

8.8.3.2.4. Direct access to the underlying cv::Mat

In some cases, one needs to assign values of elements of a data objects based on some portion of another data object. This can be done by using this method of accessing the underlying matrix (cv::Mat) of a data object directly. Following example shows the method to access underlying planes in multidimensional matrices.

// 4 x 5 x 3 DataObject, int16
ito::DataObject d4(4,5,3,ito::tInt16);
std::cout << "DataObject (4x5x3), int16 \n" << std::endl;
d4 = 3;        //assign value 3 to all elements
//access to the third plane (index 2)
int planeID = d4.seekMat(2);
cv::Mat *plane3 = (cv::Mat*)d4.get_mdata()[planeID];
std::cout << "OpenCV plane" << std::endl;
std::cout << *plane3 << std::endl;
//accessing second line in plane3
ito::int16* rowPtr2 = (ito::int16*)plane3->ptr(1);
//regions of interest
//d5 = d4[1:3,0:2,:]
ito::Range ranges[3] = { ito::Range(1,3), ito::Range(0,2), ito::Range::all() };
ito::DataObject  d5 = d4.at(ranges);
d5 = 7;

Let’s try to analyse the code above. As we can see in line #6, we used seekMat() method to retrieve the plane id of 3rd plane in 3 dimensional matrix d4.

line #7 declares a pointer variable plane3 of type cv::Mat to hold the contents of plane 3 of data object d4. Line #11 declares a row pointer to point a particular row in plane 3 of data object d4 as a revision to the previous method of accessing elements of a data object using row pointer.

line #14 defines the exemplary ranges to create a new data object d5 from a part of data object d4, which is done in line #15 with the use of at() method.

The other way to perform the same operation of line #14 is shown below.

ito::Range *ranges = new ito::Range[3];
ranges[0] = ito::Range(1,3);
ranges[1] = ito::Range(0,2);
ranges[2] = ito::Range::all();
delete ranges;

This code shows the way to modify ranges individually, which can be very useful if one needs to modify this range later in this code to work on other data objects perhaps.

Note

Please consider, that the first index of the range is the first zero-based index inside of the selected range. The second value is always one index after the last index inside of the region of interest. This is very important!! This behaviour is somehow unintuitive, however similar to OpenCV and Python.

Note

get_mdata() is a function declared under DataObject class. It returns pointer to vector of cv::_Mat-matrices.

8.8.3.2.5. Accessing all elements of a data object using iterators

There are two classes defined, called DObjIterator and DObjConstIterator respectively, under the namespace ITOM, which support the developer with an easy way to iterate through the whole data object. This method can be used only if one needs to iterate through all elements of a data object at once. Following code snippet shows the example of this method.

int temp = 0;        // Temporary variable for indexing some arrays used in this test.
ito::DataObject d6(21,13,ito::tInt16);   // Declaring a 21 x 13 data object with data type int16.
ito::DObjIterator it;    // Declaration of DObjIterator
for(it=d6.begin();it!=d6.end();++it)
{
    *((ito::int16*)(*it_2d)) = cv::saturate_cast<ito::int16>(temp++);     // Assigning a unique value to each element of a data object using iterator.
}

As can be seen in the code above, line #2 declares a 21x31 data object d6 of type int16. Line #3 declares an iterator object it of class DObjIterator. DataObject class contains being() and end() methods to work with iterators. A brief description to this methods can be found under DataObject - Reference document. These methods contains pointers to the first and last elements of any data objects respectively. Line #4 makes a meaningful use of these methods in for loop to iterate through the data object d6. We first initiate the iterator it with the pointer returned by d6.begin(), iterate through the whole data object increasing the iterator value by one in each iteration till the pointer value in iterator it reaches the pointer value of the last element of the data object checking the condition it!=d6.end().

Advantages

• This method is a compromise between its usability with ease and performance on execution level. Integration of this method in code is fast and easy.

• Developer does not think about if…else conditions to decide the boundaries of Region of Interest to access any data object.

Drawbacks

• Performance degrades against the method Addressing elements of a data object using row pointer.

• It is not advisable to use this method if one needs to access some part or a single element of a data object.

8.8.3.3. Working with data objects

Now, lets have a look on various methods to work with data objects.

8.8.3.3.1. Creating Eye Matrix

Any square data object might need to be converted in eye matrix during many operations in matrix calculations. This can be quickly done using function eye() declared under DataObject class. Syntax for the function eye() is shown below.

dataObjectName.eye(noOfDimensions, dataType);

Return Type: void

To understand the use of this function, following is an exemplary code given. Let’s have a look at it.

ito::DataObject *d2 = new ito::DataObject();
d2->eye(3, ito::tInt8);
std::cout << "3x3-eye matrix (int8)" << *d2 << std::endl;
delete d2;
d2 = NULL;

Here, the function eye() has been used with pointer variable d2 to convert the data object d2 into eye matrix.

Note

eye() function accepts only square matrices as inputs, otherwise it throws exception.

8.8.3.3.2. Creating Ones Matrix

Like Eye Matrix, Ones Matrix is equally important in matrix calculations. So we have developed a function called ones() under DataObject class to quickly convert any data object into ones matrix. Syntax for the function ones() is shown below.

dataObjectName.ones(dim 1,dim 2,…,dim n, dataType);

Return Type: void

ito::DataObject *d3 = new ito::DataObject();
d3->ones(2,3,4,ito::tFloat64);
std::cout << "2x3x4-ones matrix (double)" << *d3 << std::endl;
delete d3;
d3 = NULL;

Here, the function ones() has been used in line #2 with pointer variable d3 to convert the data object d3 into ones matrix of dimension 2x3x4.

8.8.3.3.3. Creating Zeros Matrix

We have developed a function called zeros() under DataObject class to quickly convert any data object into zero matrix. Syntax for the function zeros() is shown below.

dataObjectName.zeros(dataType);

dataObjectName.zeros(const size_t size, dataType);

dataObjectName.zeros(const size_t sizeY, const size_t sizeX, dataType);

dataObjectName.zeros(const size_t sizeZ, const size_t sizeY, const size_t sizeX, dataType);

dataObjectName.zeros(const unsigned char dimensions, const size_t *sizes, dataType);

Return Type: RetVal

As zeros() function is overloaded, there are more than one syntax shown above.

Note

The RetVal class is used for handling error management and return relative codes. More description on this class can be seen in RetVal - Reference.

Following code explains the usage of zeros() function.

ito::DataObject *dObjZeros = new ito::DataObject();
dObjZeros->zeros(2,3,4,ito::tFloat64);
std::cout << "3x4x5-zeros matrix (double)" << *dObjZeros << std::endl;
delete dObjZeros;
dObjZeros = NULL;

Here, line number 2 shows the way to use zeros() function to convert data object dObjZeros into a zero matrix.

8.8.3.3.4. Adjusting ROI of a Data Object

This section will teach you about how to adjust Region of Interest (ROI) in any data object.

The following example code shows the way to adjust ROI with adjustROI() method and to locate ROI with locateROI() method.

//adjusting ROI of 6x7 data object.
ito::DataObject d6(6,7,ito::tInt16);
int roiLocate[]= {0,0,0,0}; //Empty Array to locate ROI of 2 dimensional data object d6.
d6.adjustROI(-2,0,-1,-4);
d6.locateROI(roiLocate);
std::cout << d6 << std::endl;
for(int i =0;i<4; i++)
{
    std::cout << roiLocate[i] << std::endl;
}

Here, line #4 shows the use of adjustROI() function where negative parameters indicate that the ROI is shrinking in particular dimension. More detailed description of adjustROI() and locateROI() methods can be seen under DataObject - Reference document.

One can also pass an array as a parameter to this adjustROI() function describing the offset details as shown in the following code.

int matLimits2d[] = {-2,0,-1,-4};
d6.adjustROI(2,matLimits2d);
std::cout << d6 << std::endl;

Here, adjustROI() function is called with 2 parameters and as can be seen in line #1, the array matLimits2d[] contains the same offset values as passed in adjustROI() method in the previous example.

One can use this example to adjust ROI of data objects more than 2 dimensions as well as shown in later examples below.

The following code shows such an example to modify ROI of a 3 dimensional data object.

//adjusting ROI of 6x7x8 data object.
ito::DataObject d7(6,7,8,ito::tFloat32);
int matLimits3d[] = {-1,-2,0,-2,-3,-1};
int lims3d[]= {0,0,0,0,0,0}; //Empty Array to locate ROI of 3 dimensional data object d7.
d7.adjustROI(3,matLimits3d);
d7.locateROI(lims3d);
std::cout << d7 << std::endl;
for(int i = 0; i<5; i++)
{
    std::cout << lims3d[i] << std::endl;
}

Here, a 3 dimensional data object d7 of dimensions 6x7x8 is declared in line #1 using the implementation #4 for data objects.

As can be seen in line #3, array matLimits3d[] of return type int contains required 6 offset values to adjust ROI of 3 dimensional data object d7. As shown in line #4, an empty array lims3d[] of int as return type is defined to locate the ROI of data object d7 using locateROI() function. Line #7 will print the resultant data object after being adjusted by adjustROI() method in line #5 and the for loop in line #8-11 will print these located offset values of the resultant ROI of d7.

8.8.3.3.5. Setting and Getting Axis Units

In this section, you will study about assigning and retrieving the axis units at each dimension of a data object. setAxisUnit() method is used to assign a unit to a particular axis (dimension) of a data object and is declared under DataObject class. Syntax for this method is given below.

dataObjectName.setAxisUnit(const unsigned int axisNum, const std::string &unit);

Return Type: int

This function returns 1 if the axis does not exists.

getAxisUnit() method is used to retrieve a unit of a particular axis and is also declared under DataObject class. The syntax for this method is shown below.

dataObjectName.getAxisUnit(const int axisNum, bool &validOperation);

Return Type: std::string

This method returns Null if the axisNum is out of the range.

Following example code explains both of these methods.

ito::DataObject d8(6,7,ito::tFloat32);
bool vop1, vop2 = 0;
    d8.setAxisUnit(0,"cm");
d8.setAxisUnit(1,"cm");
std::string AxisUnit1 =d8.getAxisUnit(0,vop1); //Getting axis unit of 1st dimension of data object d8
std::string AxisUnit2 =d8.getAxisUnit(1,vop2); //Getting axis unit of 2nd dimension of data object d8
std::cout << "Axis Unit of 1st Dimension:" << AxisUnit1 << std::endl;
std::cout << "Axis Unit of 2nd Dimension:" << AxisUnit2 << std::endl;

Here, a 2 dimensional data object d8 of dimensions 6x7 is declared in line #1. Line #2 declares boolean variables vop1 and vop2 to pass as parameters in getAxisUnit() method later. Line #3 and #4 sets the units for dimensions 1 and 2 of data object d8 respectively.

These assigned axis units can be retrieved by getAxisUnit() method as shown in line #5 and #6. Line #7 and #8 prints these retrieved axis units of data object d8.

8.8.3.3.6. Setting and Getting Axis Scale

In this section, we will learn about setting and getting the scale values of particular Axis (dimension) of a data object. This can be done using setAxisScale() and getAxisScale() functions as shown below. These both functions are declared under DataObject class. Syntax for the setAxisScale() function is shown below:

DataObjectName.setAxisScale(const unsigned int axisNum, const double scale);

Return Type: int

In the same way, syntax for the getAxisScale() function is shown below.

DataObjecName.getAxisScale(const int axisNum)

Return Type: double

Following exemplary code can explain the usage of these functions in a better way.

ito::DataObject d9(6,5,3,ito::tInt16);
d9.setAxisScale(0,5);
d9.setAxisScale(1,-0.5);
d9.setAxisScale(2,3.24);
double AxisScale1 =d9.getAxisScale(0);
double AxisScale2 =d9.getAxisScale(1);
double AxisScale3 =d9.getAxisScale(2);
std::cout << "Axis 1 Scale:" << AxisScale1 << "Axis 2 Scale:" << AxisScale2 << "Axis 3 Scale:" << AxisScale3 << std::endl;

As shown in line #2-4, setAxisScale() function is used to assign scales of 5, -0.5 and 3.24 on Axis 0, 1 and 2 respectively of data object d9. Line #5-7 explains how the axis scales can be retrieved using the function getAxisScale(). Line #8 prints down these retrieved axis values at the end of this code snippet.

8.8.3.4. Copy data into an existing data object

Often, it is necessary to copy external data arrays into a region of interest, an entire plane or an entire data object. Of course this can be done using the methods from the accessing and assigning section above. However for the common case of copying 2D matrices into a two-dimensional region of interest or a 2D-plane of a data object, there exists the method copyFromData2D. The main requirement is, that the size of the data object exactly fits to the given size of the external array. Additionally, the types of the data must fit as well. Let’s describe the method using two examples:

//example for method
ito::RetVal copyFromData2D(const _Tp *data, int sizeX, int sizeY);

//create 6 uint16 values
ito::uint16 arr[] = {1,2,3,4,5,6};

//create a 3x2x3, uint16 data object filled with 0
ito::DataObject b;
b.zeros(3,2,3,ito::tUInt16);

//get a slice of the second plane (careful: index (1,2) only selects one! plane)
ito::Range ranges2[] = {ito::Range(1,2),ito::Range::all(), ito::Range::all()};
ito::DataObject c = b.at(ranges2);

//let all values of c set to the values given by the first argument
//3,2 indicates the width and height of data, since arr is a one dimensional array.
ito::RetVal ret = c.copyFromData2D(arr,3,2);

//prints the resulting overall object b, where the second plane is [1,2,3;4,5,6]
std::cout << b << std::endl;

The second example allows to only copy a subpart of the given data block into the data object

//example for method
ito::RetVal copyFromData2D(const _Tp *data, int sizeX, int sizeY, \
    const int x0, const int y0, const int width, const int height);

//create 6 uint16 values
ito::uint16 arr[] = {1,2,3,4,5,6};

//create a 3x2x3, uint16 data object filled with 0
ito::DataObject b;
b.zeros(3,2,3,ito::tUInt16);

//let the values 2,3 and 5,6 be copied into the second and third column of the second plane
//of b.
ito::Range ranges2[] = {ito::Range(1,2),ito::Range::all(), ito::Range(1,3)};
ito::DataObject c = b.at(ranges2);
ito::RetVal ret = c.copyFromData2D(arr,3,2,1,0,2,2);

//prints the resulting overall object b, where the second plane is [0,2,3;0,5,6]
std::cout << b << std::endl;

The copyFromData2D is often used for copying camera data inside an internal or an externally given data object.

8.8.3.5. Operations on data objects

In this section, we will learn some basic operations which can be performed using data objects.

8.8.3.5.1. Adjugate of a data object

In many matrix calculations, there occurs a need to adjugate a matrix. Here, we also have a function adj() declared under DataObject class, which returns an adjugated matrix of the original data object. Syntax for this method is shown below.

DataObjectName.adj();

Return Type: ito::DataObject*

Following code snippet explains the use of adj() function.

ito::DataObject d10(6,5,3,ito::tComplex128);
d10.at<ito::complex128 >(0,1,2) = cv::saturate_cast<ito::complex128 >(ito::complex128 (23.2,0));
d10.at<ito::complex128 >(1,0,1) = cv::saturate_cast<ito::complex128 >(ito::complex128 (0,3));
d10.at<ito::complex128 >(2,2,1) = cv::saturate_cast<ito::complex128 >(ito::complex128 (1234,-23.34));
ito::DataObject adjugatedDataObj = d10.adj();
std::cout << "The Adjugated data object:" << std::endl;

In the code above, a 6x5x3 data object d10 of data type ito::tComplex128 is created. Later on, in line #2-4, some complex values are assigned at data object elements (0,1,2), (1,0,1) and (2,2,1). In line #5, an adjugated matrix of data object d10 is created using adj() function and stored in new data object called adjugatedDataObj. Line #6 prints out this adjugated matrix.

8.8.3.5.2. Transpose a data object

Transposing a data object is also one of the very important techniques in matrix calculations. With the use of trans() function, we can achieve a transposed matrix of the original data object. This function is also declared under DataObject class. Syntax for this function is shown below.

DataObjectName.trans()

Return Type: ito::DataObject

Following code snippet explains the usage of trans() function.

ito::DataObject d11(2,2,ito::tInt16);
int temp=0;
for(int i=0;i<2;i++)
{
    for(int j=0;j<2;j++)
    {
        temp++;
        d11.at<ito::int16>(i,j)= cv::saturate_cast<ito::int16>(temp);
    }
}
ito::DataObject transDObj = d11.trans();
std::cout<< "The Transposed data object:" << std::endl;

In the code above, a 2x2 data object d11 of type ito::tInt16 is created. This data object d11 is initiated by assigning different values to each element. In line #11, trans() function is used to transpose this data object d11 and resulted transposed data object is stored in new data objected transDobj, which gets printed out in line #12.

Note

Transposing the data object also transposes the axis related information.

8.8.3.5.3. Squeeze a data object

The squeeze method of a data object is a convenient function to return a shallow copy of the data object where all dimensions with a size of 1 are eliminated. This does not have any impact on the underlying data of the data object but only the header information is changed. Therefore, a shallow copy is possible. The squeeze operations is often used, if another function requires for instance a two dimensional data object, but a three dimensional is given. Even, if only one plane of the three dimensional object is selected using any slicing operation (region of interest…), it is still three dimensional. After the squeeze-method however, a two dimensional object is obtained.

Example:

//3 x 3 x 2, float32 data object, all values = 0
ito::DataObject a(3,3,2, ito::tFloat32);
a = 0;

//create view or shallow copy of the first plane, using the range objects
ito::Range ranges[] = {ito::Range(1,2),ito::Range::all(), ito::Range::all()};
ito::DataObject secondPlane = a.at(ranges);

//secondPlane has a size of 1 x 3 x 2, this is squeezed
ito::DataObject squeezed = secondPlane.squeeze();

//squeezed has now a size of 3 x 2, set its first element to 2
squeezed.at<ito::float32>(0,0) = 2;

//print out the original object
std::cout << a << std::endl;

//the result is:
/* [[0,0,0;0,0,0];[2,0,0;0,0,0];[0,0,0;0,0,0]]

Note

The last two dimensions belonging to planes are never squeezed, since this would require a full recreation of the data object including a deep copy of the data.

8.8.3.5.4. Basic operators with data objects

(Same syntax can be used for other operators like ‘+’,’-‘,’=+’,’=-’, div, cross multiplication (!=), <<(shift left), >> ( shift right)) For the sake of simplicity, some arithmetic operators are overloaded to work upon data objects easily. In this section, such operators to work upon data objects are discussed in details with example codes and syntaxes. Let us start with basic Add “+” operator. Following is one example shown to add two data objects with “+” operator.

ito::DataObject d12(2,2,ito::tInt16);
ito::DataObject d13(2,2,ito::tInt16);
ito::DataObject d14(2,2,ito::tInt16);
d12= cv::saturate_cast<ito::int16>(2);
d13= cv::saturate_cast<ito::int16>(2);
d14= d12 + d13;
std::cout << "Addition of two matrix is:" << d14 << std::endl;

Here, two data objects d12 and d13 are added element-wise and the resultant data object is stored in d14. In the same way many other arithmetic, compare or bitwise operators can work with data objects. In the following, many operators are introduced that are overloaded for working with data objects as argument.

8.8.3.5.4.1. Arithmetic operators

addition and subtraction

Using the + or - operator, two data objects of the same size and same type can be added/subtracted by means of an element-wise addition/subtraction:

ito::DataObject mat3 = mat1 + mat2;
mat3 = mat1 - mat2;

The same operations can also be done inplace, such that one data object is added to or subtracted from another data object, that is directly modified:

mat2 += mat1;
mat2 -= mat1;

multiplication and division

At first, the star-operator “*” is overloaded, such it is possible to multiply a constant factor to all values of the given data object. This can also be done inplace:

ito::DataObject mat2 = mat1 * 2.0;
mat1 *= 2.0; //inplace

When using the star-operator with two data objects, one needs to know that this indicates a matrix-multiplication in the mathematical sense, hence a m x n matrix multiplied with a n x k matrix results in a m x k matrix:

ito::DataObject mat3 = mat1 * mat2;

Note

This operation is only defined for float32 and float64 datatypes.

An element-wise multiplication of two data objects of same size and type is obtained by using the mul method of the first data object:

ito::DataObject mat3 = mat1.mul(mat2);

The element-wise division is finally obtained by the corresponding div method:

ito::DataObject mat3 = mat1.div(mat2);

Note

The “div” operator can not be used to calculate inverse matrix.

8.8.3.5.4.2. Comparison operators

The comparison operators can be used to element-wisely compare the elements of two data objects of same size and type. The result of all comparisons is a data object with the same size than the compared objects but with the fixed type uint8. Depending on the comparison, this resulting matrix contains a value of 0 or 1. The comparison operators are not supported for the int8 and int32 data types (OpenCV restriction). Available operators are:

ito::DataObject result = (mat1 == mat2); //equal to
ito::DataObject result = (mat1 != mat2); //unequal to
ito::DataObject result = (mat1 < mat2); //lower than
mat1 <= mat2; //lower or equal than
mat1 > mat2; //bigger than
mat1 >= mat2; //bigger or equal than

8.8.3.5.4.3. Shift operators

Shift operators play a significant role during some arithmetic operations (i.e. division/multiplication by 2), bit level calculations, etc. The shift operators are only defined for signed or unsigned fixed point data types. A left shift can either return the resulting data object or can be done in-place. The left shift moves every element in a data object by x places to the left such that the resulting number is multiplied by two to the power of x:

unsigned int x = 2;
ito::DataObject result = mat1 << x; //left-shift
mat <<= x; //in-place

The right-shift is similar but it moves the binary number by x places to the right, hence, the number is divided by two to the power of x.

unsigned int x = 2;
ito::DataObject result = mat1 >> x; //right-shift
mat >>= x; //in-place

8.8.3.5.4.4. Bitwise operations

The bitwise operators are also executed as an element-wise operation and are defined for all data types. The participating data objects must again have the same size and type. Examples are:

ito::DataObject result = mat1 & mat2; //bitwise and-combination
result = mat1 | mat2; //bitwise or-combination
result = mat1 ^ mat2; //bitwise nor-combination

//inplace:
mat1 &= mat2;
mat1 |= mat2;
mat1 ^= mat2;

8.8.3.5.4.5. Combination of different operators

Different operators (explained above) can be used in different possible combinations with data objects for speedy calculations.

Some of the examples of such combinations are shown below.

d4 = d1 + d2 - d3;
d3 = (d1 | d2).div((d1 << 1) + d1);
d4= (d1 & d2).mul(d3 >> 2);

With the close observation of the example statements above, one can get an idea on how to use these operators in different combinations to get the desired operation done.

Note

For a full reference of the class DataObject see DataObject - Reference.